Skip to contents

Classification and Regression using Oblique Decision Random Forest

Source: R/ODRF.R
ODRF.Rd

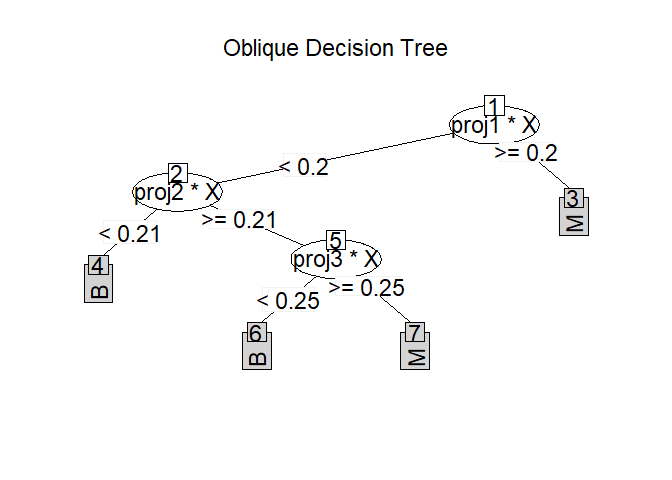
Classification and regression implemented by the oblique decision random forest. ODRF usually produces more accurate predictions than RF, but needs longer computation time.

Usage

ODRF(X, ...)

# S3 method for class 'formula'
ODRF(
  formula,
  data = NULL,
  split = "auto",
  lambda = "log",
  NodeRotateFun = "RotMatPPO",
  FunDir = getwd(),
  paramList = NULL,
  ntrees = 100,
  storeOOB = TRUE,
  replacement = TRUE,
  stratify = TRUE,
  ratOOB = 1/3,
  parallel = TRUE,
  numCores = Inf,
  MaxDepth = Inf,
  numNode = Inf,
  MinLeaf = 5,
  subset = NULL,
  weights = NULL,
  na.action = na.fail,
  catLabel = NULL,
  Xcat = 0,
  Xscale = "Min-max",
  TreeRandRotate = FALSE,
  ...
)

# Default S3 method
ODRF(
  X,
  y,
  split = "auto",
  lambda = "log",
  NodeRotateFun = "RotMatPPO",
  FunDir = getwd(),
  paramList = NULL,
  ntrees = 100,
  storeOOB = TRUE,
  replacement = TRUE,
  stratify = TRUE,
  ratOOB = 1/3,
  parallel = TRUE,
  numCores = Inf,
  MaxDepth = Inf,
  numNode = Inf,
  MinLeaf = 5,
  subset = NULL,
  weights = NULL,
  na.action = na.fail,
  catLabel = NULL,
  Xcat = 0,
  Xscale = "Min-max",
  TreeRandRotate = FALSE,
  ...
)

Arguments

X

An n by d numeric matrix (preferable) or data frame.

...

Optional parameters to be passed to the low level function.

formula

Object of class formula with a response describing the model to fit. If this is a data frame, it is taken as the model frame. (see model.frame)

data

Training data of class data.frame containing variables named in the formula. If data is missing it is obtained from the current environment by formula.

split

The criterion used for splitting the nodes. "entropy": information gain and "gini": gini impurity index for classification; "mse": mean square error for regression; 'auto' (default): If the response in data or y is a factor, "gini" is used, otherwise regression is assumed.

lambda

The argument of split is used to determine the penalty level of the partition criterion. Three options are provided including, lambda=0: no penalty; lambda=2: AIC penalty; lambda='log' (Default): BIC penalty. In Addition, lambda can be any value from 0 to n (training set size).

NodeRotateFun

Name of the function of class character that implements a linear combination of predictors in the split node. including

  • "RotMatPPO": projection pursuit optimization model (PPO), see RotMatPPO (default, model="PPR").

  • "RotMatRF": single feature similar to Random Forest, see RotMatRF.

  • "RotMatRand": random rotation, see RotMatRand.

  • "RotMatMake": users can define this function, for details see RotMatMake.

FunDir

The path to the function of the user-defined NodeRotateFun (default current working directory).

paramList

List of parameters used by the functions NodeRotateFun. If left unchanged, default values will be used, for details see defaults.

ntrees

The number of trees in the forest (default 100).

storeOOB

If TRUE then the samples omitted during the creation of a tree are stored as part of the tree (default TRUE).

replacement

if TRUE then n samples are chosen, with replacement, from training data (default TRUE).

stratify

If TRUE then class sample proportions are maintained during the random sampling. Ignored if replacement = FALSE (default TRUE).

ratOOB

Ratio of 'out-of-bag' (default 1/3).

parallel

Parallel computing or not (default TRUE).

numCores

Number of cores to be used for parallel computing (default Inf).

MaxDepth

The maximum depth of the tree (default Inf).

numNode

Number of nodes that can be used by the tree (default Inf).

MinLeaf

Minimal node size (Default 5).

subset

An index vector indicating which rows should be used. (NOTE: If given, this argument must be named.)

weights

Vector of non-negative observational weights; fractional weights are allowed (default NULL).

na.action

A function to specify the action to be taken if NAs are found. (NOTE: If given, this argument must be named.)

catLabel

A category labels of class list in predictors. (default NULL, for details see Examples)

Xcat

A class vector is used to indicate which predictor is the categorical variable. The default Xcat=0 means that no special treatment is given to category variables. When Xcat=NULL, the predictor x that satisfies the condition "(length(table(x))<10) & (length(x)>20)" is judged to be a category variable.

Xscale

Predictor standardization methods. " Min-max" (default), "Quantile", "No" denote Min-max transformation, Quantile transformation and No transformation respectively.

TreeRandRotate

If or not to randomly rotate the training data before building the tree (default FALSE, see RandRot).

y

A response vector of length n.

Value

An object of class ODRF Containing a list components:

  • call: The original call to ODRF.

  • terms: An object of class c("terms", "formula") (see terms.object) summarizing the formula. Used by various methods, but typically not of direct relevance to users.

  • split, Levels and NodeRotateFun are important parameters for building the tree.

  • predicted: the predicted values of the training data based on out-of-bag samples.

  • paramList: Parameters in a named list to be used by NodeRotateFun.

  • oobErr: 'out-of-bag' error for forest, misclassification rate (MR) for classification or mean square error (MSE) for regression.

  • oobConfusionMat: 'out-of-bag' confusion matrix for forest.

  • structure: Each tree structure used to build the forest.

    • oobErr: 'out-of-bag' error for tree, misclassification rate (MR) for classification or mean square error (MSE) for regression.

    • oobIndex: Which training data to use as 'out-of-bag'.

    • oobPred: Predicted value for 'out-of-bag'.

    • others: Same tree structure return value as ODT.

  • data: The list of data related parameters used to build the forest.

  • tree: The list of tree related parameters used to build the tree.

  • forest: The list of forest related parameters used to build the forest.

References

Zhan, H., Liu, Y., & Xia, Y. (2022). Consistency of The Oblique Decision Tree and Its Random Forest. arXiv preprint arXiv:2211.12653.

Tomita, T. M., Browne, J., Shen, C., Chung, J., Patsolic, J. L., Falk, B., ... & Vogelstein, J. T. (2020). Sparse projection oblique randomer forests. Journal of machine learning research, 21(104).

See also

online.ODRF prune.ODRF predict.ODRF print.ODRF Accuracy VarImp

Author

Yu Liu and Yingcun Xia

Examples

# Classification with Oblique Decision Randome Forest.
data(seeds)
set.seed(221212)
train <- sample(1:209, 80)
train_data <- data.frame(seeds[train, ])
test_data <- data.frame(seeds[-train, ])
forest <- ODRF(varieties_of_wheat ~ ., train_data,
  split = "entropy",parallel = FALSE, ntrees = 50
)
pred <- predict(forest, test_data[, -8])
# classification error
(mean(pred != test_data[, 8]))
#> [1] 0.03875969
# \donttest{
# Regression with Oblique Decision Randome Forest.
data(body_fat)
set.seed(221212)
train <- sample(1:252, 80)
train_data <- data.frame(body_fat[train, ])
test_data <- data.frame(body_fat[-train, ])
forest <- ODRF(Density ~ ., train_data,
  split = "mse", parallel = FALSE,
  NodeRotateFun = "RotMatPPO", paramList = list(model = "Log", dimProj = "Rand")
)
pred <- predict(forest, test_data[, -1])
# estimation error
mean((pred - test_data[, 1])^2)
#> [1] 5.840115e-05
# }

### Train ODRF on one-of-K encoded categorical data ###
# Note that the category variable must be placed at the beginning of the predictor X
# as in the following example.
set.seed(22)
Xcol1 <- sample(c("A", "B", "C"), 100, replace = TRUE)
Xcol2 <- sample(c("1", "2", "3", "4", "5"), 100, replace = TRUE)
Xcon <- matrix(rnorm(100 * 3), 100, 3)
X <- data.frame(Xcol1, Xcol2, Xcon)
Xcat <- c(1, 2)
catLabel <- NULL
y <- as.factor(sample(c(0, 1), 100, replace = TRUE))
# \donttest{
forest <- ODRF(y ~ X, split = "entropy", Xcat = NULL, parallel = FALSE)
#> Error in eval(formula[[3]]): object 'X' not found
# }
head(X)
#>   Xcol1 Xcol2          X1         X2          X3
#> 1     B     5 -0.04178453  2.3962339 -0.01443979
#> 2     A     4 -1.66084623 -0.4397486  0.57251733
#> 3     B     2 -0.57973333 -0.2878683  1.24475578
#> 4     B     1 -0.82075051  1.3702900  0.01716528
#> 5     C     5 -0.76337897 -0.9620213  0.25846351
#> 6     A     5 -0.37720294 -0.1853976  1.04872159
#>   Xcol1 Xcol2          X1         X2          X3
#> 1     B     5 -0.04178453  2.3962339 -0.01443979
#> 2     A     4 -1.66084623 -0.4397486  0.57251733
#> 3     B     2 -0.57973333 -0.2878683  1.24475578
#> 4     B     1 -0.82075051  1.3702900  0.01716528
#> 5     C     5 -0.76337897 -0.9620213  0.25846351
#> 6     A     5 -0.37720294 -0.1853976  1.04872159

# one-of-K encode each categorical feature and store in X1
numCat <- apply(X[, Xcat, drop = FALSE], 2, function(x) length(unique(x)))
# initialize training data matrix X1
X1 <- matrix(0, nrow = nrow(X), ncol = sum(numCat))
catLabel <- vector("list", length(Xcat))
names(catLabel) <- colnames(X)[Xcat]
col.idx <- 0L
# convert categorical feature to K dummy variables
for (j in seq_along(Xcat)) {
  catMap <- (col.idx + 1):(col.idx + numCat[j])
  catLabel[[j]] <- levels(as.factor(X[, Xcat[j]]))
  X1[, catMap] <- (matrix(X[, Xcat[j]], nrow(X), numCat[j]) ==
    matrix(catLabel[[j]], nrow(X), numCat[j], byrow = TRUE)) + 0
  col.idx <- col.idx + numCat[j]
}
X <- cbind(X1, X[, -Xcat])
colnames(X) <- c(paste(rep(seq_along(numCat), numCat), unlist(catLabel),
  sep = "."
), "X1", "X2", "X3")

# Print the result after processing of category variables.
head(X)
#>   1.A 1.B 1.C 2.1 2.2 2.3 2.4 2.5          X1         X2          X3
#> 1   0   1   0   0   0   0   0   1 -0.04178453  2.3962339 -0.01443979
#> 2   1   0   0   0   0   0   1   0 -1.66084623 -0.4397486  0.57251733
#> 3   0   1   0   0   1   0   0   0 -0.57973333 -0.2878683  1.24475578
#> 4   0   1   0   1   0   0   0   0 -0.82075051  1.3702900  0.01716528
#> 5   0   0   1   0   0   0   0   1 -0.76337897 -0.9620213  0.25846351
#> 6   1   0   0   0   0   0   0   1 -0.37720294 -0.1853976  1.04872159
#>   1.A 1.B 1.C 2.1 2.2 2.3 2.4 2.5          X1         X2          X3
#> 1   0   1   0   0   0   0   0   1 -0.04178453  2.3962339 -0.01443979
#> 2   1   0   0   0   0   0   1   0 -1.66084623 -0.4397486  0.57251733
#> 3   0   1   0   0   1   0   0   0 -0.57973333 -0.2878683  1.24475578
#> 4   0   1   0   1   0   0   0   0 -0.82075051  1.3702900  0.01716528
#> 5   0   0   1   0   0   0   0   1 -0.76337897 -0.9620213  0.25846351
#> 6   1   0   0   0   0   0   0   1 -0.37720294 -0.1853976  1.04872159
catLabel
#> $Xcol1
#> [1] "A" "B" "C"
#> 
#> $Xcol2
#> [1] "1" "2" "3" "4" "5"
#> 
#> $Xcol1
#> [1] "A" "B" "C"
#>
#> $Xcol2
#> [1] "1" "2" "3" "4" "5"

# \donttest{
forest <- ODRF(X, y,
  split = "gini", Xcat = c(1, 2),
  catLabel = catLabel, parallel = FALSE
)
# }